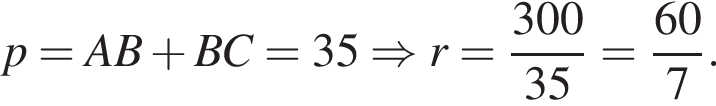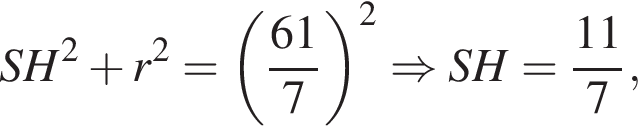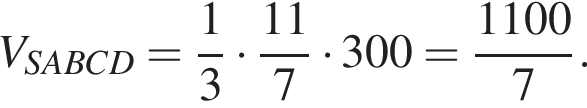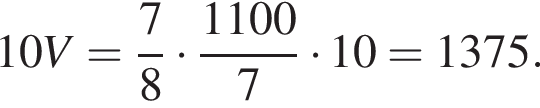Треугольник ABC — равнобедренный с основанием AB. Используя данные рисунка, найдите градусную меру угла BAC треугольника ABC.
Если вписанный угол KML изображенный на рисунке, равен 38°, то вписанный угол KNL равен:
Используя рисунок, определите верное утверждение и укажите его номер.


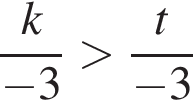
Определите, на сколько неизвестное слагаемое меньше суммы, если известно, что x + 20 = 80.
Вычислите 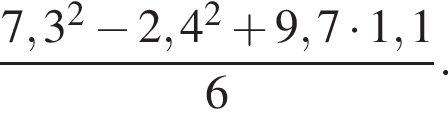
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,9 | |
| b | 108 | 7,6 |
Сумма корней (или корень, если он один) уравнения 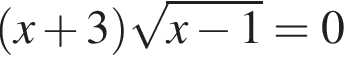 равна:
равна:
Среди данных утверждений укажите номер верного.
Значение выражения 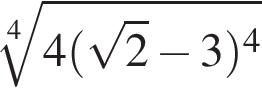 равно:
равно:
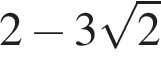
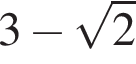
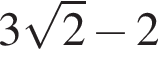
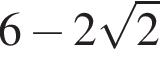
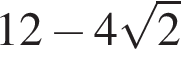
Результат упрощения выражения 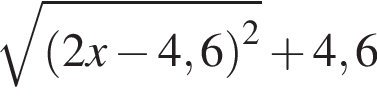 при −1 < x < 1 имеет вид:
при −1 < x < 1 имеет вид:
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура. Известно, что площадь этой фигуры составляет 28% площади некоторой трапеции. Найдите площадь трапеции в квадратных сантиметрах.
Упростите выражение 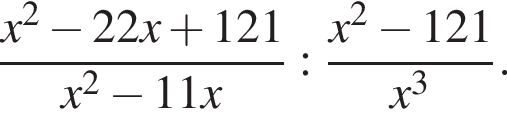
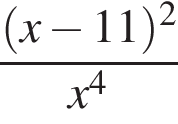
Параллельно стороне треугольника, равной 5, проведена прямая. Длина отрезка этой прямой, заключенного между сторонами треугольника, равна 2. Найдите отношение площади полученной трапеции к площади исходного треугольника.
В ботаническом саду разбили клумбу треугольной формы. Длина первой стороны клумбы равна 4 м, длина второй стороны в 2,5 раза больше длины первой, а длина третьей составляет не меньше 120% от длины второй стороны. Какому условию должен удовлетворять периметр Р (в метрах) этой клумбы.
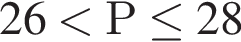

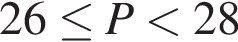

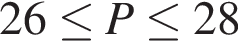
Укажите номера пар неравенств, которые являются равносильными.
1) (x − 14)2 < 0 и x − x2 − 14 ≥ 0;
2) x2 − 169 > 0 и |x| < 13;
3) x2 + x − 30 < 0 и (x − 5)(x + 6) < 0;
4) x2 ≥ 31 и 
5) 5x2 < 9x и 5x < 9.
На одной стороне прямого угла О отмечены две точки А и В так, что ОА = 1,7, OB = а, ОА < ОВ. Составьте формулу, по которой можно вычислить радиус r окружности, проходящей через точки А, В и касающейся другой стороны угла.
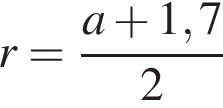
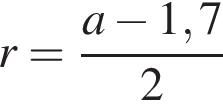
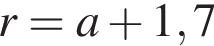
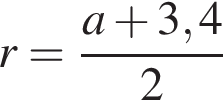
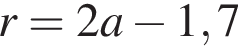
Через точку A высоты SO конуса проведена плоскость, параллельная основанию. Определите, во сколько раз площадь основания конуса больше площади полученного сечения, если SA : AO = 2 : 3.
Высоты остроугольного равнобедренного треугольника ABC (AB = BC) пересекаются в точке O. Если высота AD = 15 и AO = 10, то длина стороны AC равна:
Выберите все верные утверждения, являющиеся свойствами нечетной функции ![]() определённой на
определённой на  и заданной формулой
и заданной формулой 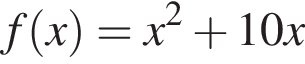 при
при ![]()
1. Функция имеет три нуля.
2. Функция убывает на промежутке [6; 9].
3. Максимум функции равен 25.
4. Минимальное значение функции равно -25.
5. 
6. Функция принимает отрицательные значения при 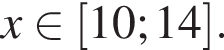
7. График функции симметричен относительно оси абсцисс.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Найдите количество всех целых решений неравенства 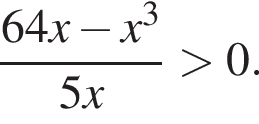
Сумма корней (или корень, если он один) уравнения 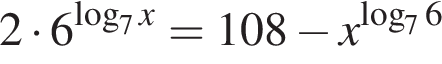 равна ...
равна ...
Найдите сумму корней (корень, если он единственный) уравнения 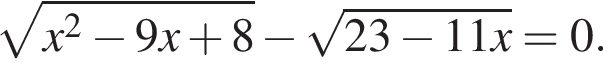
Найдите произведение корней уравнения 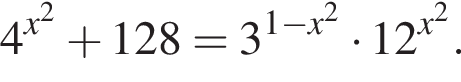
ABCD — прямоугольник. Точка N — середина стороны ВС. Отрезок DN пересекает диагональ АС в точке О (см. рис.). Найдите площадь четырехугольника ONBA, если площадь прямоугольника ABCD равна 492.
Четырёхугольник ABCD вписан в окружность. Если 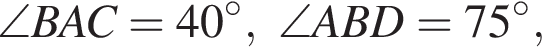 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
В основании пирамиды лежит прямоугольный треугольник, длина гипотенузы которого равна 6, острый угол равен 30°. Каждая боковая грань пирамиды наклонена к плоскости основания под углом, равным 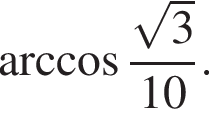 Найдите площадь боковой поверхности пирамиды.
Найдите площадь боковой поверхности пирамиды.
Найдите сумму целых значений x, принадлежащих области определения функции
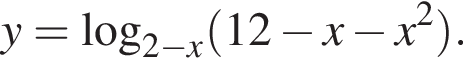
Найдите сумму всех целых чисел из области определения функции 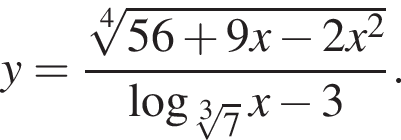
Пусть 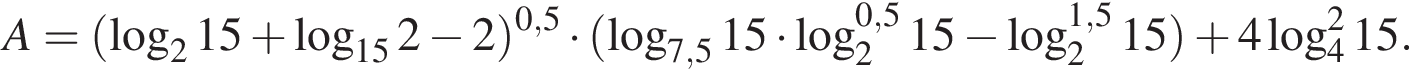
Найдите значение выражения 2A.
Прямоугольный треугольник, длина гипотенузы которого равна 10, высота, проведенная к ней, равна 3, вращается вокруг прямой, перпендикулярной гипотенузе и проходящей в плоскости треугольника через вершину большего острого угла. Найдите объем V тела вращения и в ответ запишите значение выражения ![]()
Петя записал на доске два различных натуральных числа. Затем он их сложил, перемножил, вычел из большего записанного числа меньшее и разделил большее на меньшее. Сложив четыре полученных результата, Петя получил число 1521. Найдите все такие пары натуральных чисел. В ответ запишите их сумму.
Основанием пирамиды SABCD является выпуклый четырехугольник ABCD, диагонали АС и BD которого перпендикулярны и пересекаются в точке O, АО = 9, ОС = 16, ВО = OD = 12. Вершина S пирамиды SABCD удалена на расстояние ![]() от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.
от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.

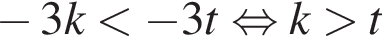 — неверно.
— неверно.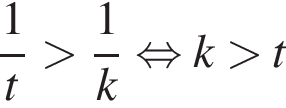 — неверно.
— неверно.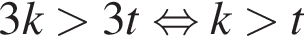 — неверно.
— неверно.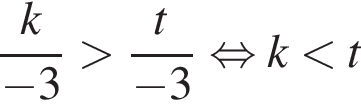 — верно.
— верно.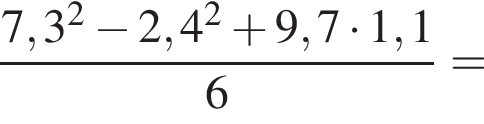
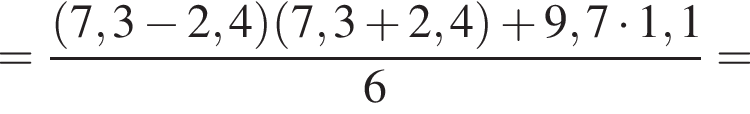
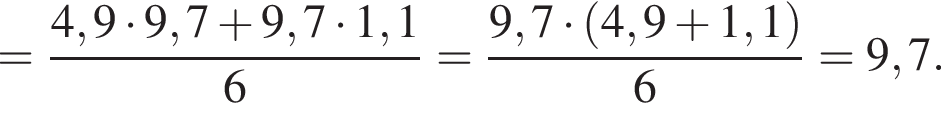
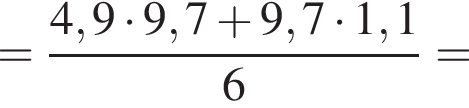
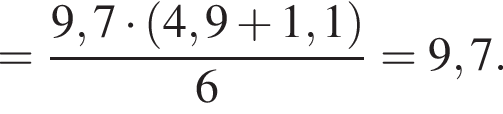
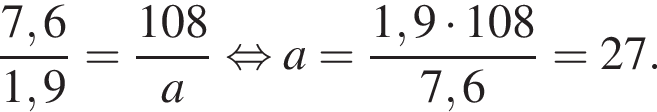
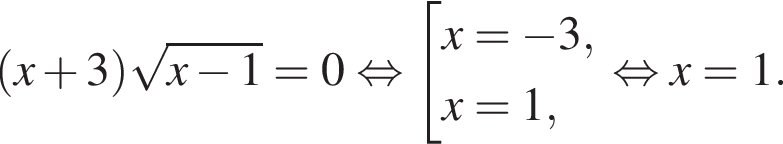
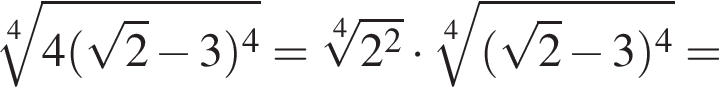
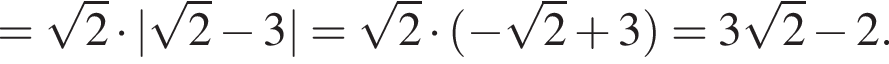

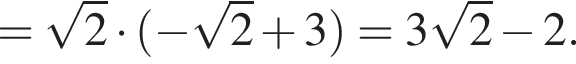
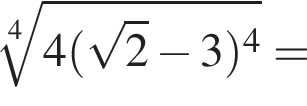
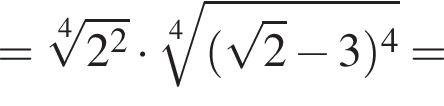
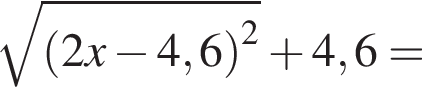
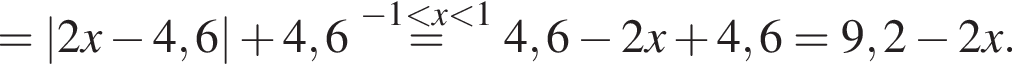
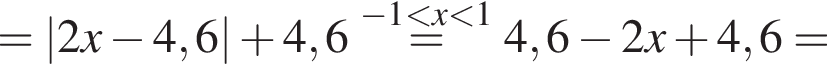
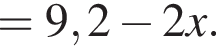
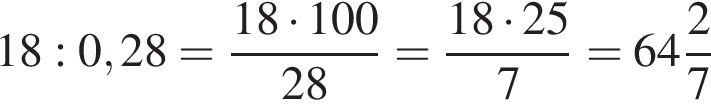 см2.
см2.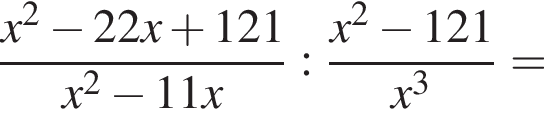
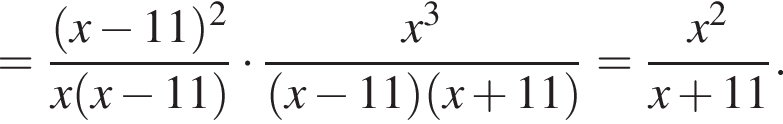
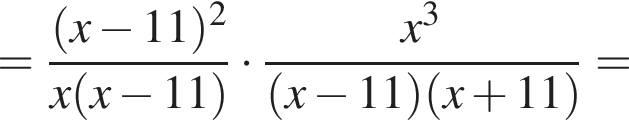
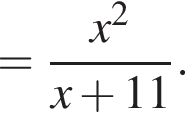
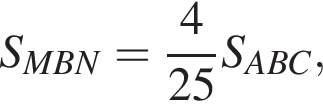 а тогда
а тогда 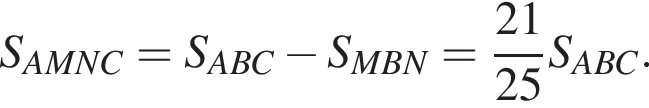
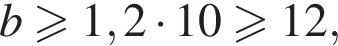 а также
а также 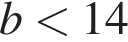 так как длина третьей стороны треугольника не может быть больше суммы двух других сторон.
так как длина третьей стороны треугольника не может быть больше суммы двух других сторон. 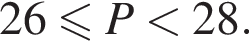
 решением второго неравенства является интервал
решением второго неравенства является интервал 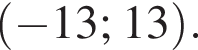 Таким образом, неравенства неравносильны.
Таким образом, неравенства неравносильны.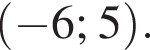 Неравенства равносильны.
Неравенства равносильны. а решением второго — полуинтервал
а решением второго — полуинтервал 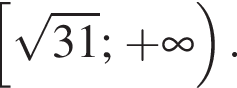
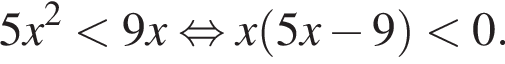 Неравенства неравносильны, так как первое неравенство имеет большее количество нулей.
Неравенства неравносильны, так как первое неравенство имеет большее количество нулей.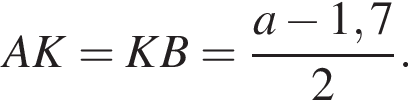
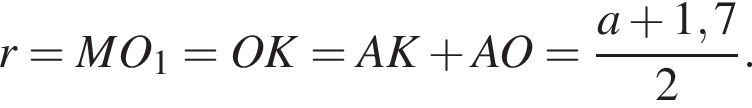
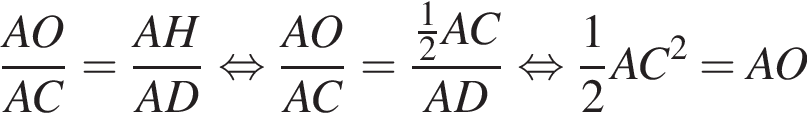
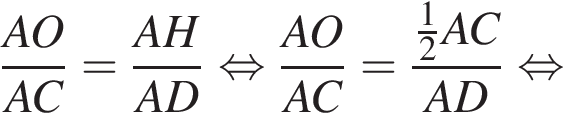
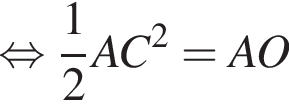

 при
при 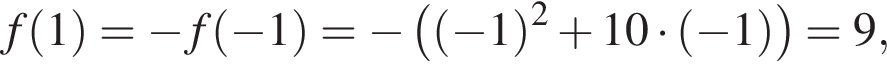
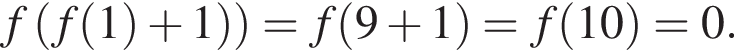 Утверждение 5 верно.
Утверждение 5 верно.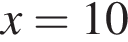 функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка
функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка 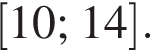 Утверждение 6 неверно.
Утверждение 6 неверно.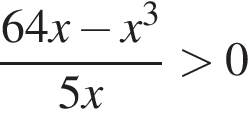
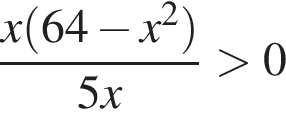
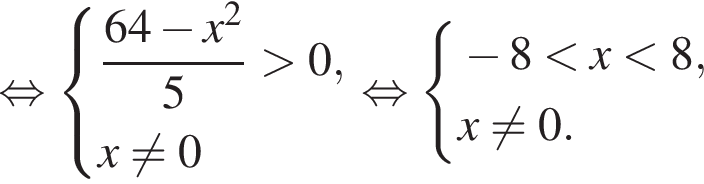
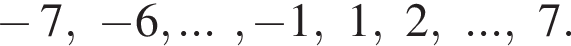
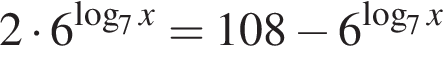
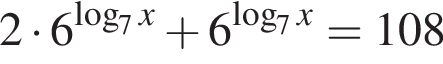
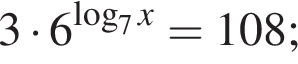
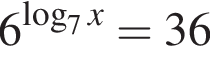
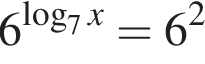
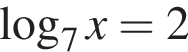
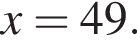
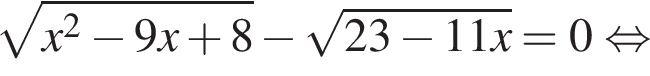
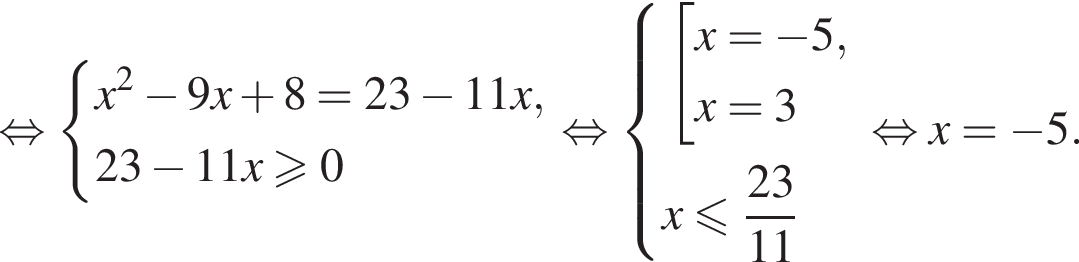
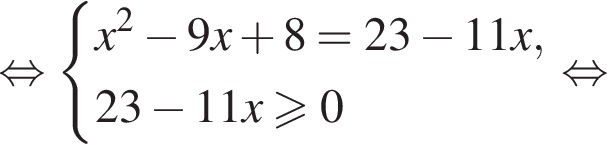
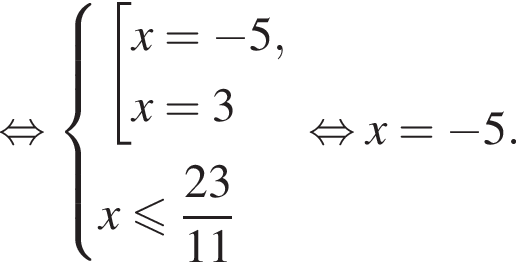
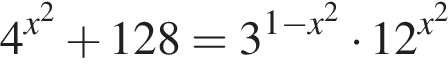
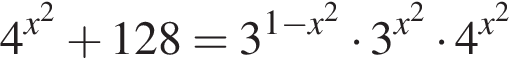
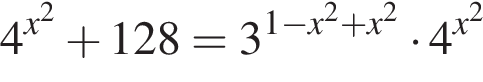
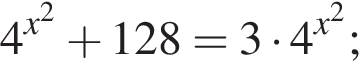
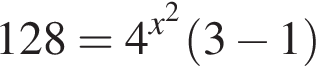
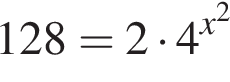
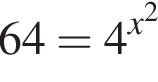
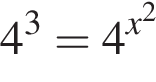
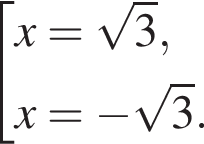
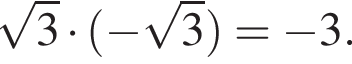
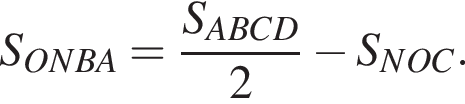 Треугольники ONC и AOD подобны по двум углам. Тогда
Треугольники ONC и AOD подобны по двум углам. Тогда 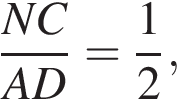 отношение площадей подобных треугольников равно квадрату коэффициента подобия, поэтому
отношение площадей подобных треугольников равно квадрату коэффициента подобия, поэтому 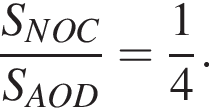 Отношение
Отношение 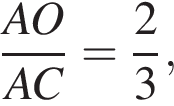 тогда
тогда 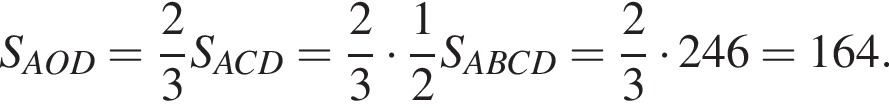
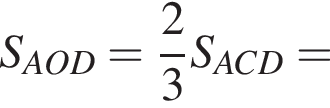
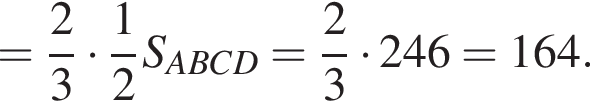
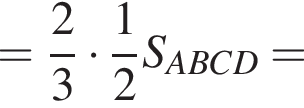
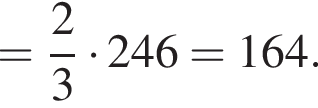
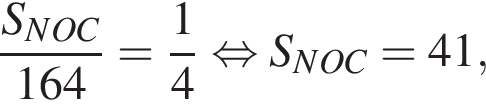 то
то 


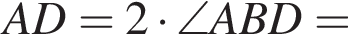

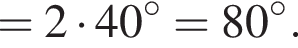
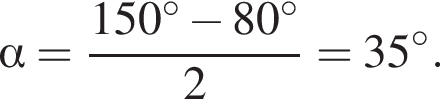
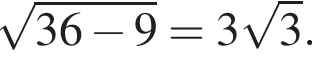 Тогда площадь основания равна
Тогда площадь основания равна 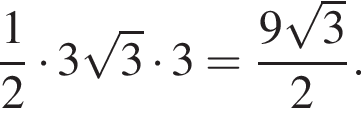
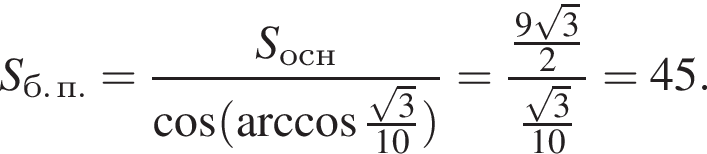
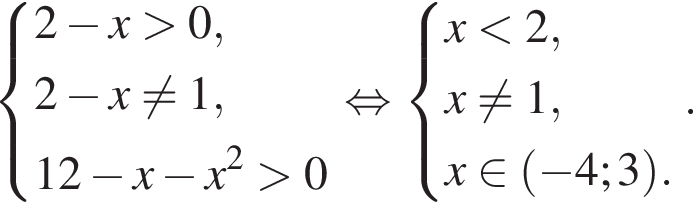
 Их сумма:
Их сумма: 
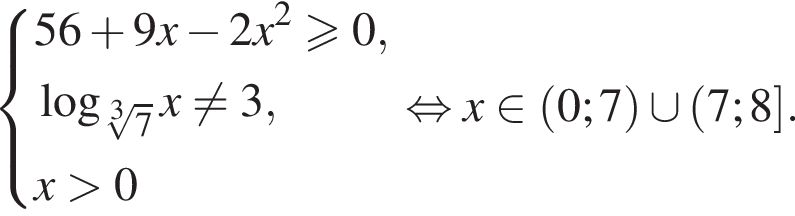

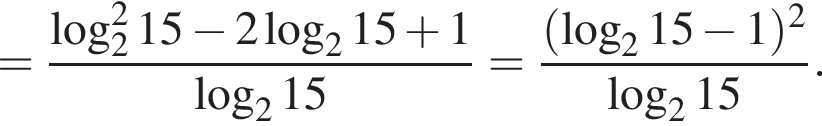
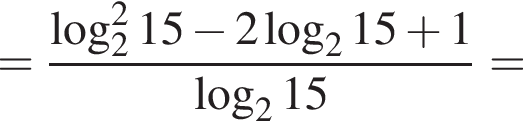
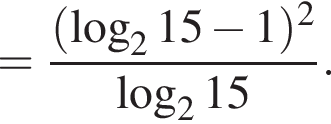
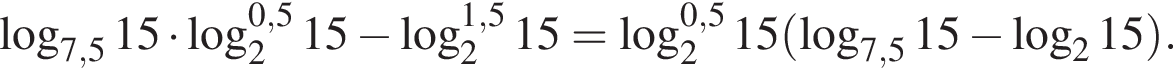
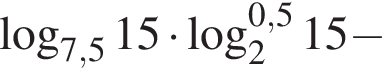
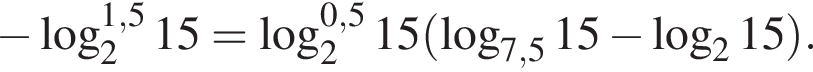
 Тогда имеем:
Тогда имеем: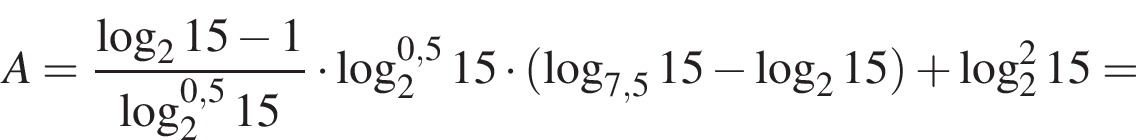
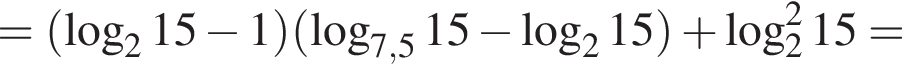
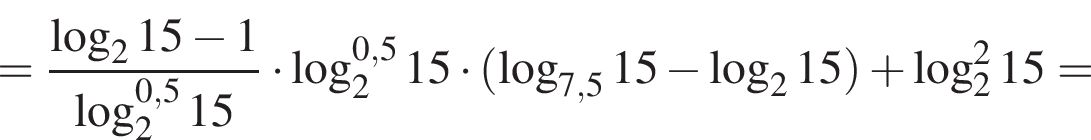
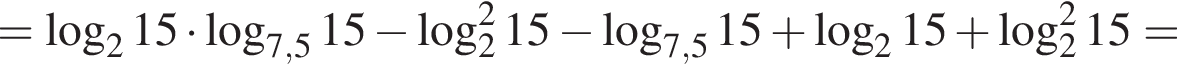
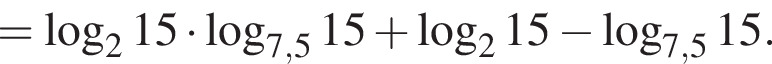
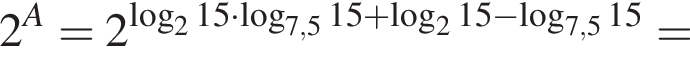
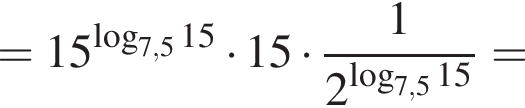
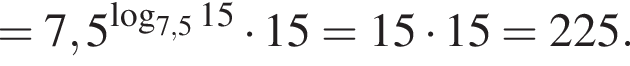
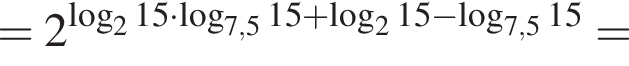
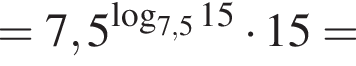
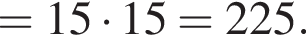
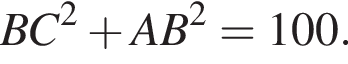 Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем:
Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем: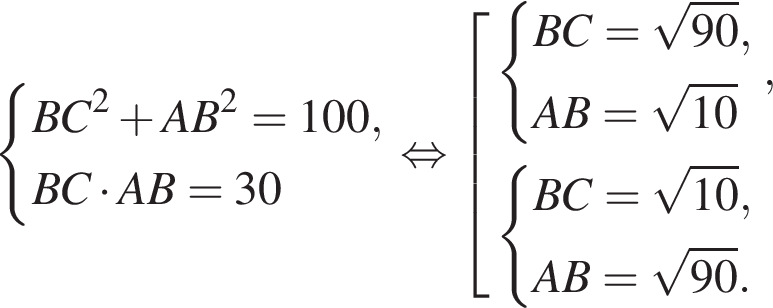
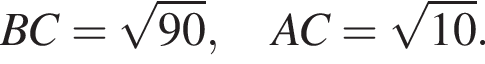 По теореме Пифагора найдем
По теореме Пифагора найдем 
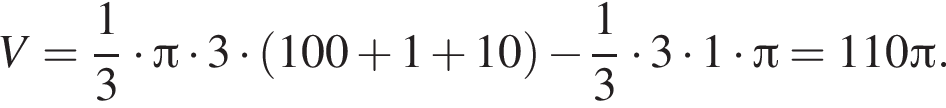
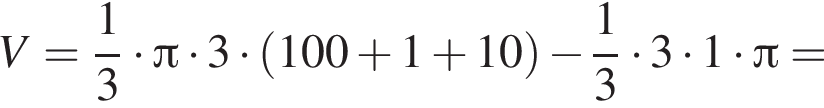
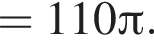
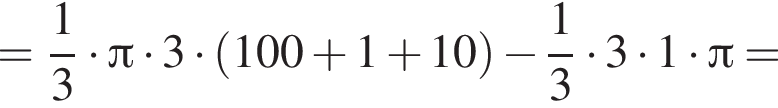
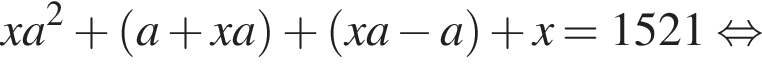
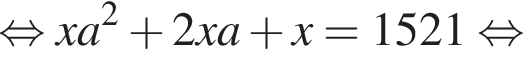

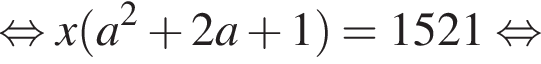
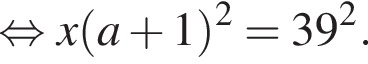
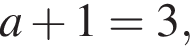
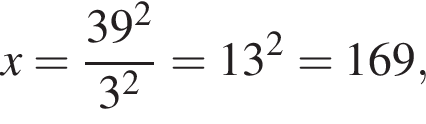
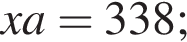
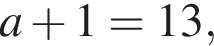
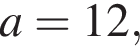
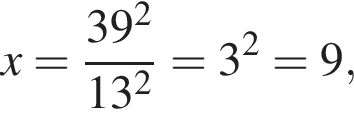
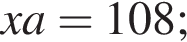
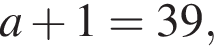
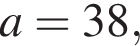
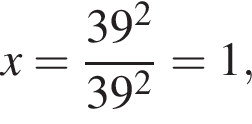
 что запрещено по условию.
что запрещено по условию.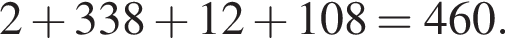
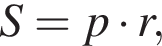 где p — полупериметр. Находим:
где p — полупериметр. Находим: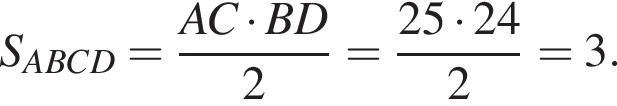
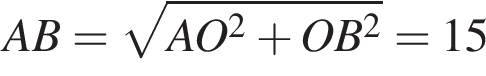 и
и 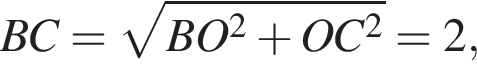 следовательно,
следовательно,